机器学习中的回归(regression)与分类(classification)问题

分类模型和回归模型本质一样，分类模型是将回归模型的输出离散化。

举几个例子:

1. Logistic Regression 和 Linear Regression：

• Linear Regression： 输出一个标量 wx+b，这个值是连续值，所以可以用来处理回归问题。
• Logistic Regression：把上面的 wx+b 通过 sigmoid函数映射到(0,1)上，并划分一个阈值，大于阈值的分为一类，小于等于分为另一类，可以用来处理二分类问题。
• 更进一步：对于N分类问题，则是先得到N组w值不同的 wx+b，然后归一化，比如用 softmax函数，最后变成N个类上的概率，可以处理多分类问题。

2. Support Vector Regression 和 Support Vector Machine:

• SVR：输出 wx+b，即某个样本点到分类面的距离，是连续值，所以是回归模型。

• SVM：把这个距离用 sign(·) 函数作用，距离为正(在超平面一侧)的样本点是一类，为负的是另一类，所以是分类模型。

3. 神经网络用于 分类 和 回归:

• 用于回归：最后一层有m个神经元，每个神经元输出一个标量，m个神经元的输出可以看做向量 v，现全部连到一个神经元上，则这个神经元输出wv+b，是一个连续值，可以处理回归问题，跟上面 Linear Regression 思想一样。

• 用于N分类：现在这m个神经元最后连接到 N 个神经元，就有 N 组w值不同的 wv+b，同理可以归一化（比如用 softmax ）变成
  N个类上的概率。

拓展： 上面的例子其实都是从 prediction 的角度举例的，如果从training角度来看，分类模型和回归模型的目标函数不同，分类常见的是 log loss, hinge loss, 而回归是 square loss。

参考：知乎：分类与回归区别是什么？

1.回归问题的应用场景

回归问题通常是用来预测一个值，如预测房价、未来的天气情况等等，例如一个产品的实际价格为500元，通过回归分析预测值为499元，我们认为这是一个比较好的回归分析。一个比较常见的回归算法是线性回归算法（LR）。另外，回归分析用在神经网络上，其最上层是不需要加上softmax函数的，而是直接对前一层累加即可。回归是对真实值的一种逼近预测。

2.分类问题的应用场景

分类问题是用于将事物打上一个标签，通常结果为离散值。例如判断一幅图片上的动物是一只猫还是一只狗，分类通常是建立在回归之上，分类的最后一层通常要使用softmax函数进行判断其所属类别。分类并没有逼近的概念，最终正确结果只有一个，错误的就是错误的，不会有相近的概念。最常见的分类方法是逻辑回归，或者叫逻辑分类。

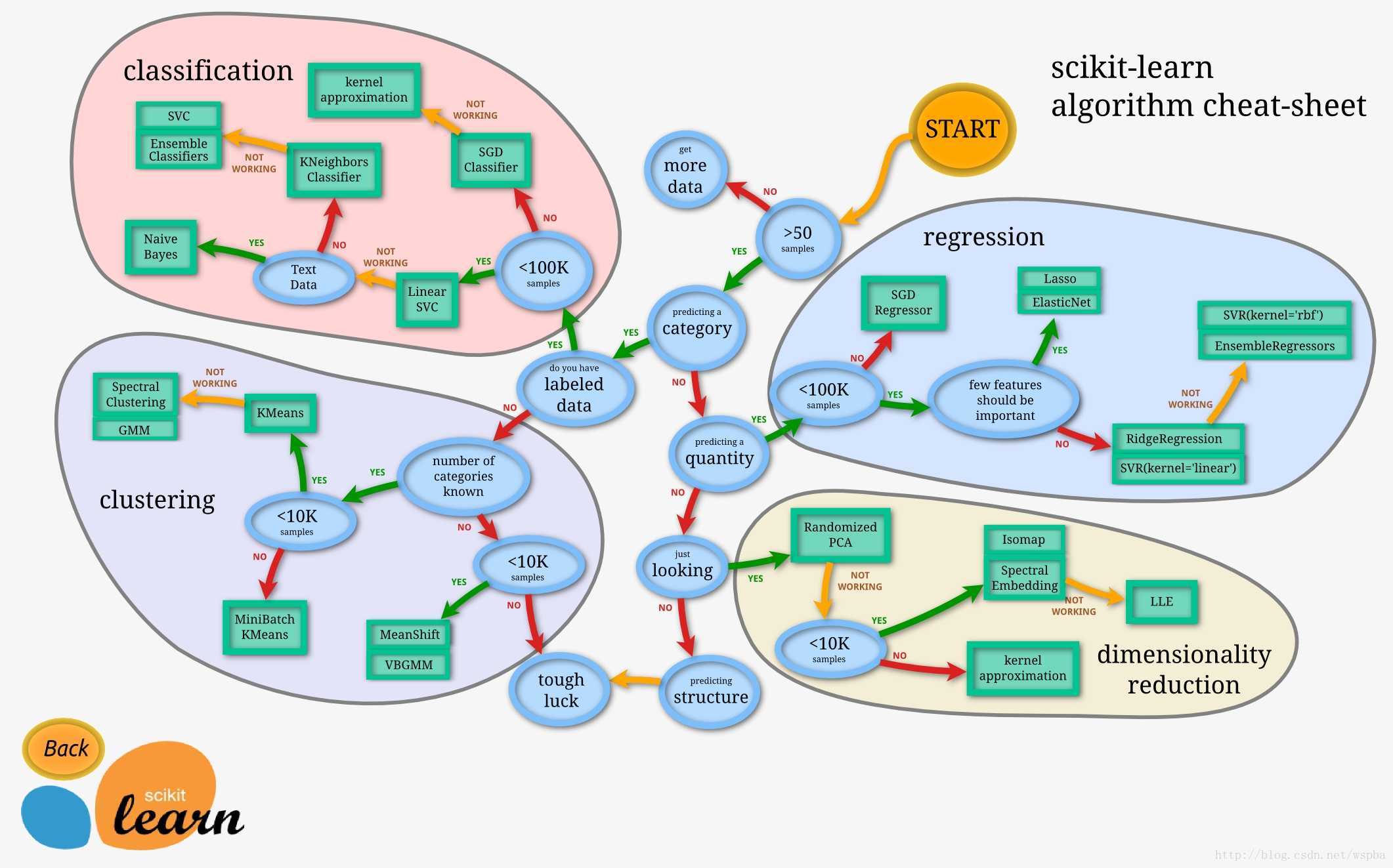
3.如何选择模型

下面一幅图可以告诉实际应用中我们如何选择合适的模型。

参考：回归(regression)与分类(classification)的区别